There are two types of basic methods that are used for solving any electrical network Nodal analysis and Mesh analysis. In this article, we are going to discuss the Nodal analysis method.
In Nodal analysis, we consider the node voltages with respect to Ground. For that Nodal analysis is also called a Node-voltage method
Table of Contents
Nodal analysis
Nodal analysis is a process that provides a general system for analyzing circuits using node voltages as the circuit element Nodal Analysis is also called the Node-Voltage Method.
The Node Voltage Method is an organized method of analyzing a circuit. It is based on Kirchhoff’s Current Law.
Definition Of Node
A node is a point where two or more branches(circuit element) are connected
Identifying Node

IN this circuit 1,2,3 are showing the node of this circuit.
Types of Nodes in Nodal analysis
- Non-Reference Node – It is a node which has a particular Node Voltage. e.g. Here Node 1 and 2 are the Non Reference nodes.
- Reference Node – Reference Node is a node which acts a reference point to all the other node. It is also called the Datum Node.
Types of reference Node
1. Chassis Ground – This type of reference node acts as a common node for more than one circuits.
2. Earth Ground – When the earth potential is used as a reference in any circuit then this type of reference node is called Earth Ground.
Node Voltage
The element voltage that appears across the terminals of a single element called a branch voltage. When we use the word node voltage, we are referring to the potential difference between two nodes of a circuit.

Consider one of the nodes in our circuit to be the reference node. All the other node voltages are measured with respect to the reference node. If node 3 is assigned as the reference node, we establish two node voltages at nodes 1 and 2.
The reference node is almost always called the ground node, and it gets a ground symbol in the schematic, as shown in the above circuit. The potential of the ground node is defined as 0V. The potentials of all the other nodes are measured relative to ground.
Solving A Circuit By Using Nodal Analysis
- Choose a node as the reference node. The voltages V1, V2… Vn-1 are assign to the remaining nodes. The voltages which are assigned to the remaining nodes are referenced with respect to the reference node.
- Apply KCL to each of the non-reference nodes.
- Apply Ohm’s law to express the branch currents in terms of node voltages.

Node Always assumes that current flows from a higher potential to a lower potential in the resistor. Hence, the current is expressed as follows

- After the application of Ohm’s Law, we get the n-1 node equations in terms of node voltages and resistances.
- Solve n-1 node equations for the value of node voltages and get the required node Voltage as a result.
Explain Briefly With a Mathematical Example
(Node Analysis With Current Source)

Calculate Node Voltages in the given circuit.
Solution:-
In the given circuit, we have 3 nodes from which one is the reference node and the other two are non-reference nodes Node 1 and Node 2.
Step 1. Assign the nodes voltages as V1 and V2 and also mark the directions of branch currents with respect to the reference nodes.
Step 2. Apply Kirchhoff’s Current Law. to Node 1 and 2
For Node 1 (pointed red)

![]()
For node 2 (pointed blue)

![]()
Step 3. Apply Ohm’s Law to equation 1

Simplifying the above equation we get
![]()
Now, Apply Ohm’s Law to equation 2

Simplifying the above equation we get
![]()
Step 4. Solve the equations 3 and 4 to get the values of V1 and V2 as

Now substituting value V2 = 20 Volts in equation 3 we get
![]()
Hence node voltages are V1 = 13.33 Volts and V2 = 20 Volts. ….(Ans)
Nodal Analysis With Voltage Source
Case 1. If a voltage source is connected between the reference node and non-reference node, we can simply set the voltage at the non-reference node equal to the voltage of the voltage source and its analysis can be done as we are done with current sources. V1 = 10 Volts.
Case 2. If the voltage source is between the two non-reference nodes then it forms a Supernode whose analysis is done as follows.
SuperNode Analysis
We used the relationship between the two nodes of the floating battery to generate a term to put in the KVL equation, plus an extra equation. Some textbooks call this a supernode. In the preceding discussion, we could have used that word, but we just resorted to our creativity to work through the puzzle.
Definition of Supernode
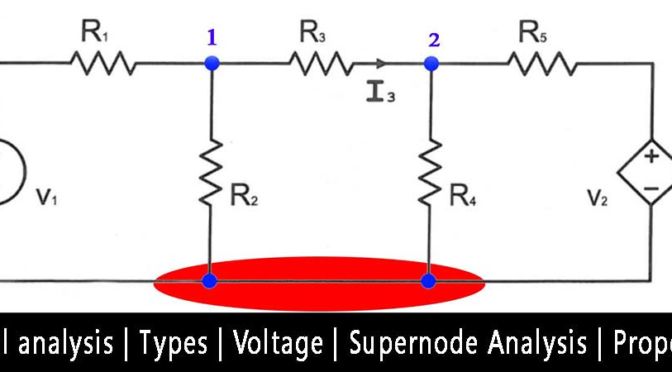
When a voltage source (Independent or Dependent source) is connected between the two non-referenced nodes then these two nodes form a generalized node called the Supernode

In the above Figure source, V2 is connected between two non-reference nodes Node 2 and Node 3. So here Node 2 and Node 3 form the Supernode.
Properties of Supernode
- The difference between the voltage of two non-reference nodes is known as Supernode.
- A supernode has no voltage of its own
- A supernode requires the application of both KCL and KVL to solve it.
- Any element can be connected in parallel with the voltage source form to the supernode.
- A Supernode satisfies the KCL like a simple node
Solve A Circuit Containing Supernode

Here 2V voltage source is connected between Node-1 and Node-2(pointed red) and it forms a Supernode with a 10Ω resistor in parallel.
Note – By connecting any element in parallel with the voltage source forming Supernode doesn’t make any difference because V2– V1 = 2V always whatever may be the value of the resistor. Thus 10 Ω can be removed and the circuit is redrawn and applying KCL to the supernode as shown in figure gives

Expressing the node voltages.


![]()
From Equation 1 and 2
![]()
Hence, V1 = – 7.333V and V2 = – 5.333V. (Ans)
Owner Of ICEEET




11 comments
Remarkable! Its truly remarkable piece of writing, I have got much clear idea on the topic of from this paragraph.
Highly energetic article, I loved that a lot. Will there be a part 2?
Wow that was unusual. I just wrote an extremely long comment but after I clicked submit my comment didn’t appear. Grrrr… well I’m not writing all that over again. Anyway, just wanted to say wonderful blog!
Excellent post. I used to be checking continuously this weblog and I’m inspired! Very useful info specifically the closing section 🙂 I care for such information a lot. I used to be seeking this certain information for a long time. Thank you and best of luck. |
[…] Nodal Analysis and Super Node for DC excitation […]
I appreciate the effort you put into compiling this informative post.
It’s well-written.
Thank you for providing such practical advice. I’ll definitely be trying out them in my personal life.
This article spoke to my heart. It captures my thoughts perfectly.
When someone writes an piece of writing he/she keeps the
plan of a user in his/her brain that how a user can understand
it. Therefore that’s why this post is outstdanding.
Thanks!
I’m not sure where you’re getting your information, but good topic.
I needs to spend some time learning much more or understanding more.
Thanks for magnificent information I was looking for this information for my mission.
After looking over a handful of the blog posts on your web page, I seriously like your way of writing a blog.
I bookmarked it to my bookmark webpage list and will be checking
back soon. Please visit my web site too and tell me how you feel.