Mesh analysis

The mesh analysis is also called the Loop Current Method, is quite similar to the Branch Current method in that it uses simultaneous equations, KVL  (Kirchhoff’s Voltage Law), and Ohm’s Law to determine unknown currents in a circuit. It disagrees from the Branch Current method in that it does not use KCL (Kirchhoff’s Current Law), and it is usually able to solve a circuit with less unknown variables and less synchronous equations, which is especially nice if you’re forced to solve without a calculator.

Identify Loops And Meshes

The first step in the Mesh Current method is to identify loops within the circuit enclose, all components. In our example circuit, the loop formed by E₁, R₁, and R₂ will be the first while the loop formed by E₂, R₂, and R₃ will be the second. The strangest part of the Mesh Current method is envisioning circulating currents in each of the loops. In fact, this method gets its name from the idea of these currents meshing together between loops like sets of circling gears.

The selection of each current’s direction is entirely free just as in the Branch Current method, but the resulting equations are easier to solve if the currents are going the same direction through intersecting element (note how currents I₁ and I₂ are both going up through resistor R₂, where they mesh or intersect). If the assumed direction of a mesh current is wrong, the answer for that current will have a negative value.

Loop Current

It is clear that i1 is the current flowing in source V1 and resistor R1. Likewise, i2 is the current flowing in resistor R2 and source V2. But what is going on with the current in R3?

Let’s take a close-up look at R3  in the middle branch of the circuit. What is the element current flowing through R3?

Step To Analysis The Mesh Current

1.  Check whether there is a possibility to transform all current sources in the given circuit to voltage sources.
2. Set the current directions to each mesh in a given circuit and follow the same direction for each mesh.
3.  Apply and simplify the KVL equations to each mesh.
4.  Solve the simultaneous equations of various meshes to get the mesh currents and these equations are exactly equal to the number of meshes present in the circuit.
5. Consider the below DC circuit to apply the mesh current analysis, such that currents in various meshes can be found. In the below figure there are three meshes  ACDA, CBDC and ABCA but the path ABDA is not a mesh. As a first step, the current through each mesh is assigned in the same direction as shown in the figure.

Secondly, we have to apply KVL for each mesh. By applying KVL around the first loop we get

V1 − V3 − R2 ( I1 − I 3 ) − R4 ( I1 − I 2 ) = 0

V1 − V3 = I1 ( R2 + R4 ) − I2R4 − I3R2 ………………(1)

Similarly, applying KVL around the second loop we get,

−V2 − R3 ( I 2 − I 3 ) − R4 ( I 2 − I1 ) = 0

− V2 = − I1R4 + I 2 ( R3 + R4 ) − I 3 R3 ………………………(2)

And by applying KVL around the third loop we get,

V3 − R1I 3 − R3( I 3 − I 2 ) − R2( I 3 − I1 ) = 0

V3 = − I1R2 − I2R3 + I3(R1 + R2 + R3) ………………………(3)

Therefore, by solving the above three equations we can obtain the mesh currents for each mesh in the given circuit.

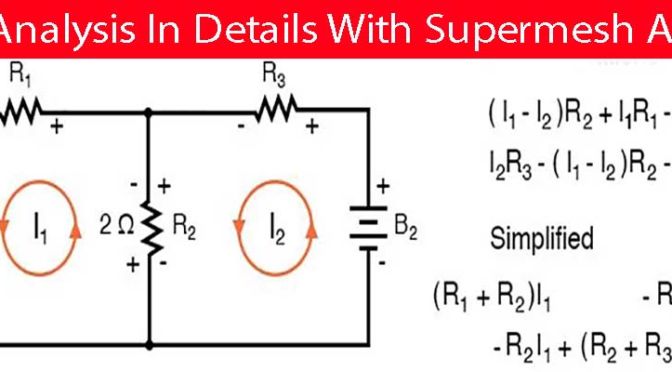
Super Mesh Analysis

 Super mesh Analysis is a better technique instead of using Mesh analysis to analysis such a complex electric circuit, where two meshes have a current source as a common element. This is same where we use Supernode circuit analysis instead Nodal circuit analysis to simplify such a circuit where the assign supernode, completely enclosing the voltage source inside the supernode and reducing the number of none reference nodes by one for each voltage source.

A super mesh is formed when two adjacent meshes share a common current source and none of these (adjacent) meshes contains a current source in the outer loop.

In super mesh analysis technique, the current source is in the inner area of the super mesh. Therefore, we are able to reduce the number of meshes by one for each current source which is present in the circuit.

Consider the below circuit in which super mesh is formed by the loop around the current source.

The current source is common to the meshes 1 and 2 and hence it must be analyzed independently. To achieve this, assume the branch that contains the current source is open-circuited and create a new mesh called super mesh.

Applying KVL to the super mesh we get

V = I1R1 + (I2 – I3) R3

= I1R1 + I2R3 – I3R3

Applying KVL to the Mesh 3 we get

(I3 – I2) R3 + I3R4 = 0

And the difference between the two mesh currents gives the current from the current source. Here the current source direction is in the loop current direction I1. Hence I1 is more than I2, then

I = I1 – I2

Thus, by using these three mesh equations we can easily find the three unknown currents in the network.

​

Owner Of ICEEET

Engr. Mizan

See author's posts

Summary

Article Name

Mesh Analysis In Details With Supermesh Analysis

Description

The mesh analysis is also called the Loop Current Method, is quite similar to the Branch Current method in that it uses simultaneous equations...

Author

Mizan

Publisher Name

ICEEET

Publisher Logo