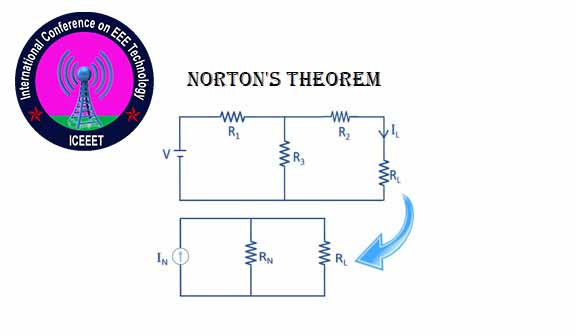
Norton’s Theorem: Norton’s Theorem is a very popular method for solving complex circuits, as well as Thevenin’s Theorem. We have already discussed the Thevenin’s Theorem in detail. Today we will discuss in detail the Norton Theorem.
What is going on in our discussion today:
- Something about Norton’s Theorem / Norton Theorem Discovery.
- Norton’s Theorem Statement.
- Steps to apply the Norton Theorem.
- Circuit solution with Norton Theorem.
Table of Contents
Something about Norton’s Theorem Discovery
Edward Laurie Norton While researching the Thevenin Theorem, Bell Lab found that a complex circuit could also be expressed through current sources and parallel resistances.
After several tests, he finally 1926 About four years after the discovery of Thevenin’s Theorem, that is, he published his Theorem. But sadly that year, Thevenin Theorem’s inventor Leon Charles Thevenin He died, leaving no comment on Norton’s Theorem on his behalf.

Norton Theorem Statement
Norton stated in his theory that “any two-terminal linear bilateral dc network can be replaced by an equivalent circuit consisting of a current source and a parallel resistor”.

Steps to apply the Norton Theorem
To solve a circuit using the Norton Theorem, we need to take some steps or Steps Have to follow. For the sake of interpretation, we do not assume from the lower circuit RL To find the current flowing through it.

So now let’s not know the solution steps or the steps to solve the above circuit with Norton Theorem:
Step 1: The load in which the current is to be removed must be shortened. (Figure 2)

Step 2:The route that has been shortened by the route flows through Norton Current(RN) Have to find out
Step 3:Now this short path has to be opened. If there is a voltage source, you need to short and open the current source. Then this circuit will be Norton Resistance(RN) Have to find out

Step 4: The latest IN, RN And RL In addition to this, Norton’s Equivalent Circuit has to be calculated and this new circuit IL It has to be evaluated.

Load current, IL = (RN×IN / RN+RL)
Circuit Solutions with Norton Theorem:
Q: From the following circuit using the Norton Theorem a b Draw Norton’s Equivalent Circuit at the terminal.

Solution: First we have a b terminal RL Who made it short.

This time it flows through Norton Current(IN)Find out,
.·. IN = 9 / 3 = 3 Amps.
After that IN The short path opens and 9 V Norton Resistance from the lower circuit by shortening the associated voltage source (RN) Have to find out

Since 3Ω And 6Ω Norton Resistance will be in parallel,
RN = 3 ।। 6
⇒ RN = (3 × 6) / (3 + 6)
⇒ RN = 18 / 9
.’. RN = 2 Ω
So Norton’s Equivalent Circuit will be as follows:

Reference by,