Kirchhoff’s Voltage Law | Kirchhoff’s Loop Rule | Divider Circuits

Just like the current source of the Kirchoff, the voltage source of the Kirchoff is very important. The combination of these two sources and Ohm’s formulas forms the basis of electrical circuit theory. So to understand a circuit, one must understand these three sources very well.

We divided the discussion on the Karshoff formula into two parts. Today is the 2nd or last part of it.

What’s going on in today’s discussion: 

• The voltage of the curves is the formula.
• Strategies and explanations for solving the voltage source of cursive.
• Circuit solution using the voltage formula

The voltage of the curves is the formula

Kirchoff said in his voltage source,

The algebraic sum of all the voltages present in a closed-loop will be zero.

That is, the amount of voltage inside the closed-loop will be algebraically solved by solving them algebraically.

We can also say that the amount of voltage change inside the closed loop is zero.

That is the change in voltage, ΔV = 0.

When applying a voltage formula, the voltage has to be taken to Clockwise or Counter Clockwise

The voltage of the curves is the formula  (KVL) Solutions and Explanations:

At the time of the solution, a closed-loop of the circuit must take a clockwise or counter clock. Then start from a branch and proceed according to the loop. If the positive direction of the loop direction and voltage source is in the same direction then the source should be treated as negative. Again, if the negative direction of the loop direction and voltage source are in the same direction, then the source should be considered positive.

For example, in case of a voltage drop in the direction of the current, the direction of the loop direction and current direction are on the same side, then the voltage drop of this resistance will be negative. Again, if the loop direction and current direction are opposite, then the voltage drop of this resistance will be positive.

The following example will help you understand this issue a little better.

If we catch the clockwise loop in the circuit above, then the voltage that we get from the circuit is,

-V₁, +V₂, +V₃, –V₄ And +V₅

As an example, if we will 3 If we start traveling from the number branch, we will see a positive terminal first and that is. +V_{3 ,} If 4If I start from the number branch, then it is a negative terminal –V₄ Will get Similarly, if we apply the voltage formula in the circuit above, we will find,

-V₁ + V₂ + V₃ – V₄ + V₅ = 0

If we rearrange,

V₂ + V₃ + V₅ = V₁ + V₄

That is, voltage drop = voltage rise

So, we can say that the amount of voltage inside the closed-loop increases as the voltage decreases so that the sum is zero.

The voltage drop in a circuit can be easily applied by applying a voltage formula.

Circuit solution with curves voltage formula:

First, we will solve a very simple circuit.

Question 1: From the following circuit V₃Find out.

Solution:

Given,

E = 18 V

V₁ = 6 V

V₂ = 4 V

V₃ = ?

If we assume loop clockwise, then the circuit will below.

Now when I apply KVL to the circuit,

    -E + V₁ + V₂ + V₃ = 0

Or, -18 V + 6 V + 4 V + V₃ = 0

Or, -18 V + 10 V + V₃ = 0

Or, V₃ = 18 V – 10 V

 .·. V₃ = 8 V(Answer)

This time we will solve another circuit.

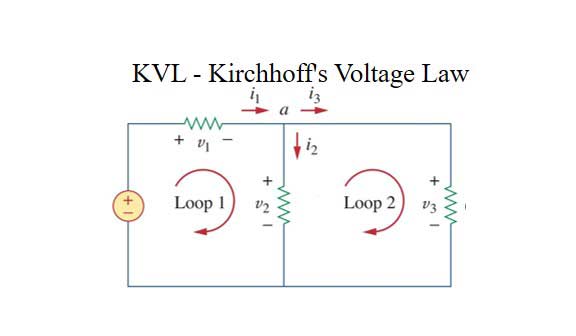
Question 2: The following circuit shows a loop. This will be the loop I₁And I₂ Find out its value.

Solution:

To solve the figure, we have two arrows Aki and Arrow as shown in figure I₁, I₂ Mark as

Now loop I₁ I’ll keep moving.

First, we have a voltage source which is 6 volts. But here the loop direction entered through the negative end of the battery and came out with the positive end. So we will write – 6 V. Then on our way there are 2-ohm registers.

We know that from Ohm’s formula. V = IR.

Here,

R = 2 Ohm and  I = I₁.

So, the voltage V = I * R

= 2 I₁.

Then there is another 4-ohm resistor. It can be written  4 I₁.

But if you notice, 4 Through the ohm register I₂ Current is flowing in the opposite direction. So 4 The voltage across the ohm register will be

4I₁ – 4I₂

= 4(I₁ – I₂).

now I₁ There is nothing else besides the mark. Now we I₁ Write the equation of the loop in the following way,

-6V + 2I₁ + 4(I₁ – I₂)

Or, -6V + 2I₁ + 4I₁ – 4I₂

Or, -6V + 6I₁ – 4I₂ ………….. (1)

Now let us loop I₂ Have to move on

I₂ Starting from the mark comes the first 3 Ohm register. I have to write it for 3 I₂. How 4 Ohm registers to write, 4I₂ – 4I₁ = 4 (I₂ – I₁).

This time I₂ Write the equation of the loop as follows,

3 I₂ + 4 (I₂ – I₁).

Or, 3 I₂ + 4 I₂ – 4 I₁

Or, 7 I₂ – 4 I₁ ……….. (2)

Now we will solve equation two. In this case, equation (1) with k 2 and equation (2) k 3 If you multiply and subtract,

0 + I3 I2 = I2

Or, I2 = 12/13

Or, I₂ = 0.9 A.

Now,I₂ Its value 1 If we put the number equation,

I₂ I₁ – 8 × 0.9 = 12

Or, I₂ I₁ – 7.2 = 12

Or, I₁ = (1₂ – 7.2) / 12

Or, I₁ = 0.4 A.

Therefore,  I₂ = 0.9 A And I₁ = 0.4 A (Answer)

Reference Books:

Introductory Circuit Analysis Book by Robert L Boylestad 

Fundamentals of Electric Circuits Book by Charles K. Alexander and Matthew N.O. Sadiku

Electronics-Tutorial website

Owner Of ICEEET

Engr. Mizan

See author's posts