Norton Theorem

Table of Contents

The Norton theorem reduces the networks equivalent to the circuit having one current source, parallel resistance, and load. Norton’s theorem is the converse of Thevenin’s Theorem. Its formation of the equivalent current source instead of an equivalent voltage source as in Thevenin’s theorem. The determination of internal resistance of the supply network is identical in each the theorems.

In the last stage that is in the equivalent circuit, the current is placed in parallel to the internal resistance in Norton’s Theorem whereas in Thevenin’s Theorem the equivalent voltage source is placed in series with the internal resistance.

Statement: Any two-terminal DC network can be replaced by an equivalent circuit consisting of a current source and a parallel resistance.

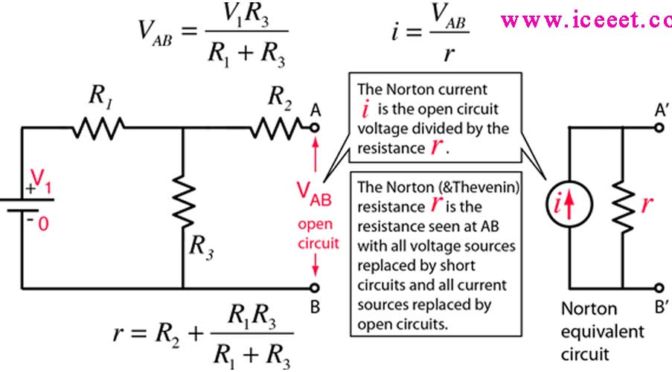
Explanation of Norton’s Theorem

To understand Norton’s Theorem thoroughly, allow us to contemplate a circuit diagram given below-

In order to find the current through the load resistance I_L as shown in the circuit diagram above, the load resistance has to be short-circuited as shown in the diagram below

Now, the value of current I flowing in the circuit is found out by the equation

And the short-circuit current I_SC is given by the equation shown below

Now the short circuit is transferred, and the independent source is deactivated as shown in the circuit diagram below and the value of the internal resistance is calculated by

As per the norton theorem, the equivalent source circuit would contain a current source in parallel to the internal resistance, the current source being the short-circuited current across the shorted terminals of the load resistor. The Norton’s Equivalent circuit is represented as.

Lastly, the load current I_L calculated by the equation shown below-

Where,

The I_L is the load current
The I_sc is the short circuit current
The R_int is the internal resistance of the circuit
The R_Lis the load resistance of the circuit

Step For Solving a Circuit By Norton’s Theorem

Step 1 – The load resistance of the circuit is removed.

Step 2 – Determine the internal resistance R_int of the source network by deactivating the constant sources.

Step 3 – Now short the load terminals and find the short circuit current I_SC flowing through the shorted load terminals using conventional network analysis methods.

Step 4 – Norton’s equivalent circuit is drawn by keeping the internal resistance R_int in parallel with the short circuit current I_SC.

Step 5 – Again connect the load resistance R_L of the circuit across the load terminals and find the current through it is known as load current I_L.